8 Hydroelectricity

Figure 8.1. Nant-y-Moch dam, part of a 55 MW hydroelectric scheme in Wales. Photo by Dave Newbould, [www.origins-photography.co.uk](http://www.origins-photography.co.uk).

To make hydroelectric power, you need altitude, and you need rainfall. Let’s estimate the total energy of all the rain as it runs down to sea-level.

For this hydroelectric forecast, I’ll divide Britain into two: the lower, dryer bits, which I’ll call “the lowlands;” and the higher, wetter bits, which I’ll call “the highlands.” I’ll choose Bedford and Kinlochewe as my representatives of these two regions.

Let’s do the lowlands first. 1 To estimate the gravitational power of lowland rain, we multiply the rainfall in Bedford (584 mm per year) by the density of water (1000 kg/m3), the strength of gravity (10 m/s2) and the typical lowland altitude above the sea (say 100 m). The power per unit area works out to 0.02 W/m2. That’s the power per unit area of land on which rain falls.

Erratum. Kinlochewe is shown incorrectly. The correct location is about 60km further north.

When we multiply this by the area per person (2700 m2, if the lowlands are equally shared between all 60 million Brits), we find an average raw power of about 1 kWh per day per person. This is the absolute upper limit for lowland hydroelectric power, if every river were dammed and every drop perfectly exploited. Realistically, we will only ever dam rivers with substantial height drops, with catchment areas much smaller than the whole country. Much of the water evaporates before it gets anywhere near a turbine, and no hydroelectric system exploits the full potential energy of the water. We thus arrive at a firm conclusion about lowland water power. People may enjoy making “run-of-the-river” hydro and other small-scale hydroelectric schemes, but such lowland facilities can never deliver more than 1 kWh per day per person.

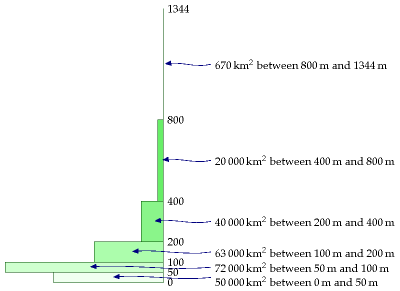
Figure 8.2. Altitudes of land in Britain. The rectangles show how much land area there is at each height.

Let’s turn to the highlands. Kinlochewe is a rainier spot: it gets 2278 mm per year, four times more than Bedford. The height drops there are bigger too – large areas of land are above 300 m. So overall a twelve-fold increase in power per square metre is plausible for mountainous regions. The raw power per unit area is roughly 0.24 W/m2. 2 If the highlands generously share their hydro-power with the rest of the UK (at 1300 m2 area per person), we find an upper limit of about 7 kWh per day per person. As in the lowlands, this is the upper limit on raw power if evaporation were outlawed and every drop were perfectly exploited.

Figure 8.3. Hydroelectricity.

Figure 8.4. A 60 kW waterwheel.

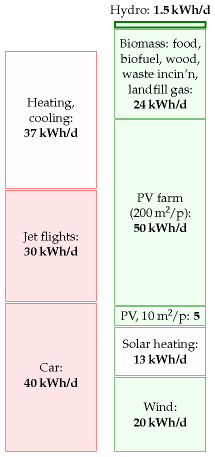
What should we estimate is the plausible practical limit? Let’s guess 20% of this – 1.4 kWh per day, and round it up a little to allow for production in the lowlands: 1.5 kWh per day.

The actual power from hydroelectricity in the UK today is 0.2 kWh/d per person, 3 so this 1.5 kWh/d per person would require a seven-fold increase in hydroelectric power.

Notes and further reading

  1. Rainfall statistics are from the BBC weather centre.↩
  2. The raw power per unit area [of Highland rain] is roughly 0.24 W/m2. We can check this estimate against the actual power density of the Loch Sloy hydro-electric scheme, completed in 1950 (Ross, 2008). The catchment area of Loch Sloy is about 83 km2; the rainfall there is about 2900 mm per year (a bit higher than the 2278 mm/y of Kinlochewe); and the electricity output in 2006 was 142 GWh per year, which corresponds to a power density of 0.2W per m2 of catchment area. Loch Sloy’s surface area is about 1.5 km2, so the hydroelectric facility itself has a power per unit lake area of 11 W/m2. So the hillsides, aqueducts, and tunnels bringing water to Loch Sloy act like a 55-fold power concentrator.↩
  3. The actual power from hydroelectricity in the UK today is 0.2 kWh per day per person. Source: MacLeay et al. (2007). In 2006, large-scale hydro produced 3515 GWh (from plant with a capacity of 1.37 GW); small-scale hydro, 212 GWh (0.01 kWh/d/p) (from a capacity of 153 MW). In 1943, when the growth of hydroelectricity was in full swing, the North of Scotland Hydroelectricity Board’s engineers estimated that the Highlands of Scotland could produce 6.3 TWh per year in 102 facilities – that would correspond to 0.3 kWh/d per person in the UK (Ross, 2008). Glendoe, the first new large-scale hydroelectric project in the UK since 1957, will add capacity of 100 MW and is expected to deliver 180 GWh per year. Glendoe’s catchment area is 75 km2, so its power density works out to 0.27 W per m2 of catchment area. Glendoe has been billed as “big enough to power Glasgow.” But if we share its 180 GWh per year across the population of Glasgow (616 000 people), we get only 0.8 kWh/d per person. That is just 5% of the average electricity consumption of 17 kWh/d per person. The 20fold exaggeration is achieved by focusing on Glendoe’s peak output rather than its average, which is 5 times smaller; and by discussing “homes” rather than the total electrical power of Glasgow (see p329).↩